안녕하세요.

고1수학내신 공부법을 알려주는 개념원리 풀자입니다.

오늘은 고등수학(하)에 나오는 첫 번째 단원인

집합에 대해서 얘기를 해보려고 하는데요.

처음 고등수학하를 선행하기 시작할 때,

누구나 한 번쯤 가졌던 의문이 있습니다.

‘집합은 왜 배울까?’, ‘

왜 집합을 제일 먼저 배우는거지?’

라는 생각이죠.

그리고 대부분 고1수학내신을 준비하는

학생들의 독특한 특징 중 하나가

가장 자신있는 수학 단원을 물어보면

‘집합'을 얘기합니다.

집합이 가장 중요해서 그런걸까요?

아니면 집합이 가장 배우기 쉬워서 그런 걸까요?

사실 학생들이 가장 집합을 가장 쉽다고 생각하는 이유는

1학기 성적을 보고 가장 학습에 열의가 높은 시점에

고등수학(하)에서 처음 배우는 단원이

‘집합'단원이기 때문입니다.

그래서 그런지 대부분의 학생들의 문제집이나

교과서의 앞부분만 때가 타 있는 경우가 많았죠.

그래서 상대적으로 앞부분만 공부를 많이 한 친구들에겐

자연스럽게 집합이 쉽게 느껴졌을 것이라고 생각합니다.

​집합은 왜 배울까?

그렇다면 두 번째 의문인

‘도대체 우린 집합을 왜 먼저 배우는 걸까?’를

설명해보자면,

집합은 다른 단원에 비해서

다른 단원과의 연계성이 적다고 느끼기 때문에

다들 이런 의문을 가질 만 하다고 생각합니다.

집합이 수학에 편입된 것은 엄청 오래되진 않았지만,

대부분의 수학에 집합을 대입해서

이론을 전개하기 시작했습니다.

그래서 대부분의 수학 이론의 토대가 집합이 되었고

이론과 개념을 증명하는 부분에선

집합을 많이 사용하고 있습니다.

실제 모의고사에서 집합 개념이 들어가는 문제는,

개념을 확인하여 참/거짓을 판별하고

옳은 개념을 구분하는 문제가

자주 나온다는 것을 알 수 있습니다.

많은 학생이 쉽다고 착각하지만,

실제 모의고사에 나오면 개념이

조금이라도 부족한 친구들은

풀기 까다로운 유형의 문제로 탈바꿈하게 되고,

학생들은 생각지도 못하게 틀리는 경우가 자주 발생하죠.

집합의 의미와 개념?

그렇다면 집합의 의미는 뭘까요?

우린 이미 일상생활에서 ‘집합’의 의미를 알고 있습니다.

집합이란

‘명확한 기준에 의하여 주어진 대상들의 모임'

이란 뜻입니다.

​

명확한 기준에 의해서 원소들을 모으며,

그 안에서 무엇이든 가지고 놀 수 있게 됩니다.

집합은 하나의 ‘범위'를 설정하여,

‘이 안에서 이것만 가지고 놀아~’

라고 하는 것과 비슷합니다.

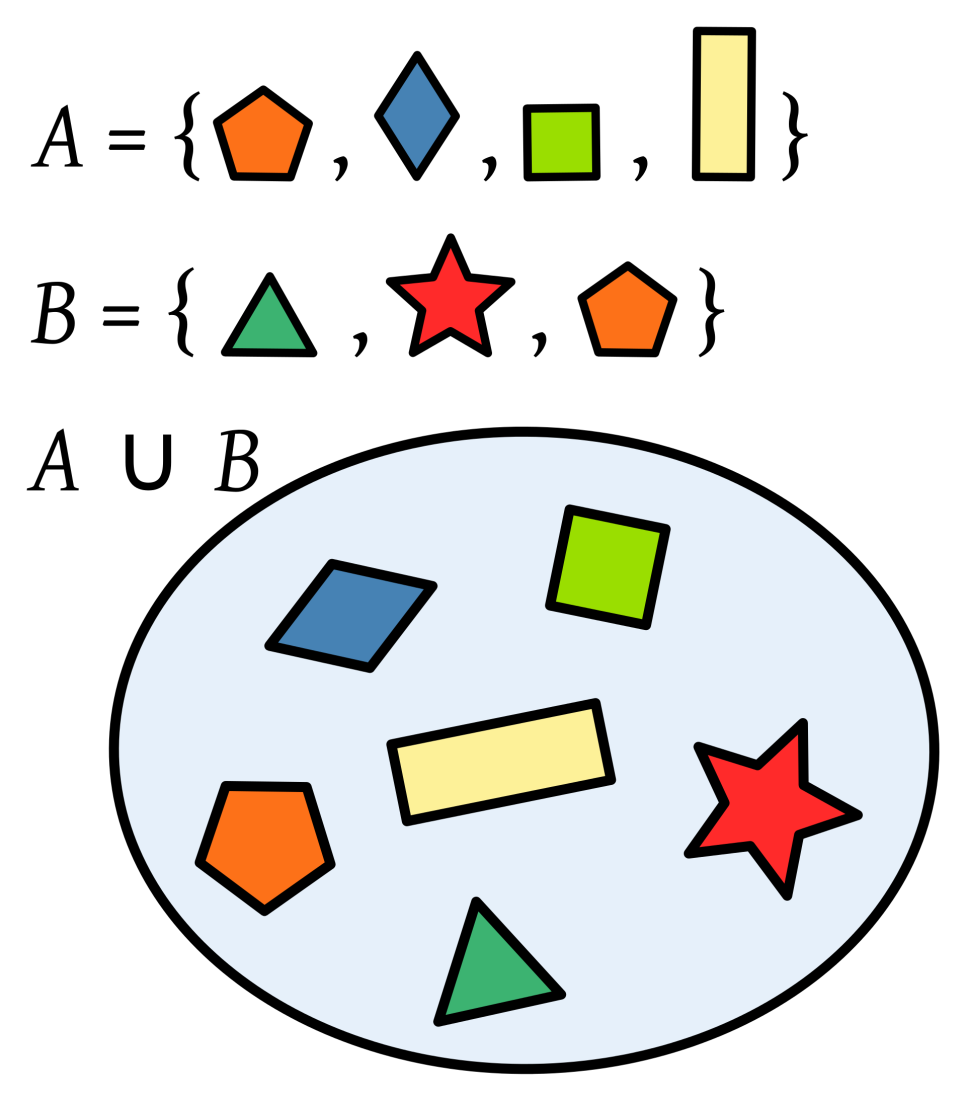
예를 들면 ‘동그라미, 세모, 네모만 가지고 그림을 그려봐' 라고 했을때,

우린 어떤 ‘동그라미,세모, 네모'

라는 정확한 범위가 주어지게 되고

그 도형만 가지고

아래와 같은 그림도 그릴수가 있게 됩니다.

('동그라미, 세모, 네모가 모여서' 책 표지)

하지만 위의 그림에서 기존에 안내해준 범위를 무시하고

하트 모양을 더해서 그린다면

명확한 범위를 설정한 집합을

무시하는 형태가 되는 것입니다.

위의 예시를 수학에 적용하면,

문제 안에 이 범위가 명확하게 설정됩니다.

위의 개념을 집합의 개념으로 정확히 알고 있으면

문제를 풀거나 실수를 바로 잡을때

편할 것이라고 생각되니

꼭 명심해 두세요:)

실제 문제로 예시를 들어보겠습니다.

--------------------------------------

10에서 100까지 자연수 중에

3과 5로 나누어 떨어지지 않는

자연수의 개수를 구하라

---------------------------------------

이런 문제가 나왔을 경우,

문제를 잘 읽고 파악하는 게 무척 중요합니다.

대부분의 학생들은 여기서 ‘구하라'라는 단어에 주목하여

3과 5로 나누어떨어지지 않는 자연수를 구하려고 하고,

대부분 거기서 실수가 시작됩니다.

‘10에서 100까지의 자연수'라는 조건을

명확하게 이해하지 않고

범위를 착각한다면 아무 생각 없이

1-9까지의 숫자를 포함하여

답으로 구하게 되고 오답이 발생합니다.

​

실수가 아닌 실력

​

오답이 나온 친구들이 자주 하는 말로

‘아... 실수로 1의 자리까지 구해버렸네요.’ 라고 할테지만

이건 실수가 아니라 집합의 개념을

정확하게 이해하지 못 한겁니다.

집합은 모든 수학의 토대가 되는 만큼

문제에서 나온다면 내가 가지고 놀 수의 범위를

특정해준다는 특징이 있습니다.

학년이 올라가게 되면 이 범위를

쉽게 특정하지 못하게 하기 위해

여러 속임수들이 나올 것이고

그것을 구분하기 위해선

집합의 개념을 정확하게

이해하는 것이 무척 중요합니다.

​

집합에 관련된 모의고사 문제가 어렵다면,

고1수학내신을 준비 할때부터

개념을 잘 정리하는 것을 추천합니다.

다른 단원과는 달리 연산의 개념보다는

이론과 이해가 필요한 단원이기 때문에

복잡한 부분이나 어려운 부분을 반드시 확인하고

미리 정리해 놓는 것이 필요합니다.

결국에 고1수학내신을 준비하는 단계를 살펴보면

허술하게 넘어갈 단원이 하나도 없다는 것을 알게 됩니다.

수학은 가성비가 떨어지는 과목이고

급성장이 어려운 과목이기 때문에

항상 꾸준하게 학습하고

자기주도학습 습관을 미리부터 들여놔야 합니다.

만약 집합을 대충 넘어갔던 고1이 있다면

반드시 복습을 하시고,

이제 선행을 시작하는 예비고1이라면

꼼꼼하게 개념을 정리해보세요.

오늘 정리해드린 집합의 개념이

도움이 되었길 기원합니다.

다음에도 다양한 개념을

이해하기 쉽게 정리해 보겠습니다!

개념원리 풀자로 알아보는

고1수학내신 집합편 이었습니다.

감사합니다:)