안녕하세요!

개념원리의 온라인 수학 학습법

풀자입니다 🥳

이번엔 중학생이나 고등학생이

수학 내신대비를 위해 알고 가면 좋을

'수 체계'에 대해서 이야기 해보려고 해요.

초등학교를 지나 중학교에 올라오면서부터

우리는 더 많은 수들에 대해 배우게 되죠.

또, 이 수들을 이용해 방정식의 해를 찾거나

포함관계를 이용하여 문제를 풉니다.

수 체계는 학년이 높아지고

과정이 늘어날 수록 계속해서 확장되고,

아래 표처럼 중등에서 배운 수의 체계는

고등에서 당연시하게 연계되기 때문에

학습을 진행할때 용어와 연계성을

잘 알아 두고 자신 있게 말할 줄 알아야 해요 💡

특히, 고등 수학 과정은 중등 과정을

복습하며 학습하는 과정이 아닌,

기본 개념 위에 확장을 시키는 과정으로

중학생때 기본 개념에 대한 학습이

제대로 되어있지 않다면,

고등수학 과정 속에서 어려움을 겪을 수 있어요 🥲

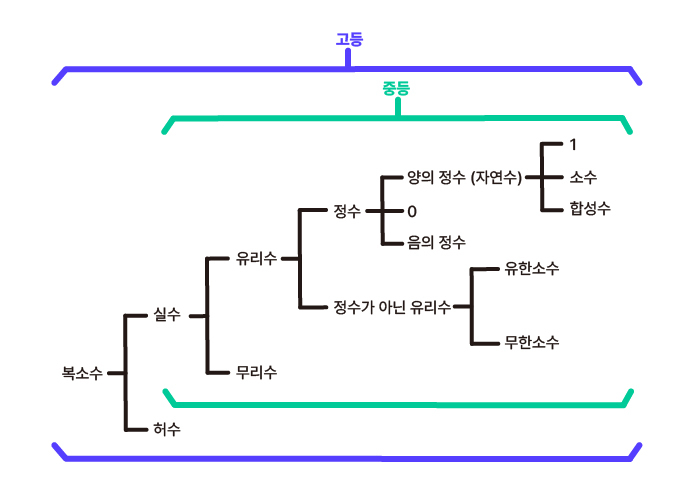
그럼 오늘 풀자와 함께 수 체계가

어떻게 확장되고 이어지는지

각 과정별로 살펴볼까요? 🧐

1. 중학 과정 수 체계의 중요성

중학교 1학년이 되면

맨 처음 새로 배우게 되는 것이

원래 알던 수에 -가 붙은

“음수” 라는 개념입니다.

자연수와 0까지 배운 초등과정이후

수체계가 확장되는 것이죠!

양의 정수(우리가 아는 자연수)와

음의 정수, 0을 합하여 “정수” 라는 큰 틀 을 배우고

이 “정수” 를 제외하고

분수로 표현 할 수 있는 모든 수를 포함 해

“유리수” 라고 합니다.

이 때 +와 -기호를 가지고

사칙연산을 하게 되는데

이는 앞으로 나올 모든 수학에

가장 기본적인 계산이자

후에 문자를 사용한 연산에서

기본으로 필요한 지식이 됩니다.

중학교 3학년이 되면

무리수 부분을 처음으로 학습합니다.

무리수는 실수 중 유리수가 아닌 수들,

즉 순환하지 않는 무한소수를 말합니다.

이 때 제곱근 = 루트(√)를 처음 배우고

제곱근을 사용한 연산도 같이 배우게 됩니다.

간혹 제곱근의 연산은할 줄 알지만

아래의 개념을 헷갈려 하는 학생들이 있는데요,

연산도 중요하지만 개념을 모른다면

전혀 의미가 없어요!

이렇게 중등과정에서 유리수와 무리수를

배우며 실수 전체를 학습하게 되는데요,

중학교 때 까지는

각각의 수 범위 내에서의 개념을 알고

기본 계산 익히는 것이 가장 중요한 이유는

고등학교에 올라가

수 체계나 기본 연산을 연습하기엔

시간적으로 무리가 있기 때문입니다.

그리고 모든 수학의 기초이기도 하지요.

따라서, 중학교때 이러한 수 체계에 대한

기초가 제대로 잡혀 있지 않다면,

당연하게 고등과정에서 수학내신대비와

모의고사 대비는 어려울 수 밖에 없겠죠? 😥

2. 고등과정과 중학 과정의 연계성

그리고 중학교때 이러한 기초과정을 지나,

고1 수학 (상)에서 처음으로 허수를 배웁니다.

물론 수학(상) 내신 시험에서는 출제되지만

사실 허수는 수학(하) 이후 교육과정에

직접적인 연계는 되지 않습니다.

하지만 수학(하) 1단원 집합과 명제에서

수 체계를 이용한 집합의 포함관계,

명제 문제 등에서

꽤 많은 빈도로 출제되고 있습니다.

그럼 수학(하) 1단원 집합과 명제에서

실제로 문제가 어떻게 출제되는지 볼까요?

​

문제 1

위의 문제는

고등수학(하) > 1. 집합과 명제 > 합집합과 교집합

에 관한 문제인데요, 포함관계를 알기 전에

기본적으로 소수, 합성수, 정수의 개념을 알고 있어야

집합 A, B, C의 원소들을 파악할 수 있습니다.

​

이때 각 용어에 대한 개념이

헷갈린다면 당연히 다시 외워야 하겠지만

가장 좋은 것은 수 체계가 어떻게 되는지

계속해서 복습을 해 놓아

언제든 수의 체계에 대해

이야기할 수 있어야 합니다.

​

​

그럼 다른 단원에서는 어떻게 활용되는지

한 문제 더 볼까요? 

문제 2

↑

고등수학(하) > 2. 함수 > 무리함수에

관한 문제인데요,

문제에서 “실수가 되도록” 이라고 하였으니

제곱근(루트)안의 값이

0보다 크거나 같아야 합니다.

알아낸 x의 범위를 이용해서

정수 x의 개수를 구하는 문제입니다.

​

함수에서는 정의역, 공역, 치역의 범위를

수의 범위로 조건을 주는 문제들이 많습니다.

​

이 문제 역시 개념을

제대로 파악해 놓지 않으면

문제에서 풀이방식의 여러시도는 뒤로한 채

문제조차 해석하지 못하는

경우가 생길 수 있어요. ☹️

​

​

3. 수학 개념용어정리는 필수

학생들이 실전문제를 풀 때는

본인이 모른다는 것을

잘 자각하지 못해요.

또, 수학은 암기과목이 아니라고 생각하죠.

​

그러나 수에 대한 개념을 물어보거나

조건으로 나오게 되는 문제에서

헷갈려 하는 학생들이 많은데요,

이러한 기본 개념에 쓰이는

용어 정리는 무.조.건 필수입니다.

수학의 가장 기본적인 뼈대이고

어떻게 이어지는지 수 체계를 그릴 수 있어야

후에 수학을 이해하고 문제를 풀어내는 데에

도움이 될 것이에요. 🙌

​

다음 시간에도 더 유익한 내용으로 찾아올게요.

그럼, 오늘도 풀자와 열공하세요! 😊